How to calculate magnetic declination and magnetic bearing:
When
you are using a compass, the needle pointing north is actually not pointing to
north. The needle is in fact pointing to the magnetic north pole which is
situated roughly north-east of Canada. It shifts every year by approximately 56km.
There
is always a difference between the True North, which is at the North Pole, and
the magnetic north. However, this difference (angle) between magnetic and true north changes every year. This
change is known as the magnetic declination.
When
using a topographic map true north is always at the top of the map. To measure
the bearing from one point to the next, the protractor must be aligned so that
0° point to the top of the map (true north). Draw a straight line from your starting point
to the end point. Place the protractor on the map, with 0° pointing to the top
of the map. Use the line connecting the two points to read the degrees from the
protractor. Remember to measure in a clockwise direction from the top.
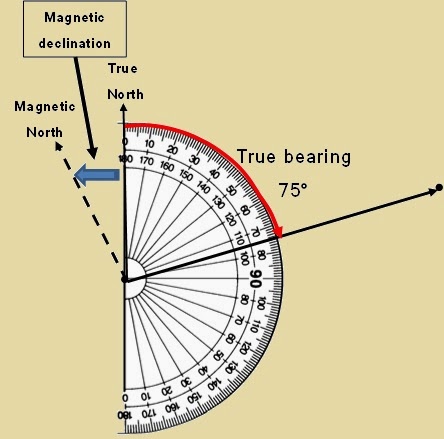
Let us assume the true bearing is 75°. If a person starts to drive in in a bearing
of 75° he will still miss his final destination. Why? You still have to add the
difference between True North and Magnetic North, also known as the magnetic
declination. Every year the magnetic north shifts, either in a westerly or
easterly direction. For an observer in South Africa the Magnetic North will
always be west from True North (North Pole). At the bottom of a topographic
map (e.g. 1:50 000) you will see a north-south arrow. Next to the north-south
arrow the mean magnetic declination and the mean annual change will be indicated. For example: “Mean magnetic
declination 16°3’ West of True North (Feb, 2019). Mean annual change 2’
Westwards (2008-2013)
So,
how do you calculate the magnetic bearing?
Step 1: Determine the true bearing
E.g. 75°
Step 2: Determine
the difference in years between the current year and the year the Magnetic declination was measured (on
topographic map)
E.g.
2024 – 2019 = 5 years
Step 2: Calculate the total magnetic change
E.g. 5 years x 2’ West = 10’ West (On the topographic map the change is 2’ West every year)
Step 3: Calculate the current magnetic declination
E.g. 16°3’ West
+ 0°10’ West When the
mean annual change is west you +, and if the change is East, you –.
16°13’ West Therefore,
the magnetic declination for 2024 is 16°13’ west from True North.
Step 4: Calculate the magnetic bearing
E.g. True Bearing + Current Magnetic
Declination
= 75° + 16°13’
= 91°13’
How to calculate real distance on a map:
This is a very easy calculation! With a ruler and calculator you can do this in three easy steps.
Use the following formula:
You will divide by a 1000 if you need the real distance in meters OR divide by a 1000 000 if you need the real distance in kilometers!
E.g. on a 1:50 000 Topographic map the map distance between Point A and Point B is 47mm.What is the real distance in kilometers?
Distance = Map distance in mm x map scale
1000 000
= 47mm x 50 000
1000 000
= 2,35km
You can also take the map distance in centimeters and multiply it by 0.5
E.g. 4.7cm x 0.5 = 2.35km
How to calculate gradient on a topographic map:
How do you calculate the gradient between two points on a 1:50 000 topographic map?
Use the following formula
Step 1: Determine the difference in altitude between the two points
E.g. point A = 1120m and Point B = 1380m
Difference in height = 1380m – 1120m = 260m
Step 2: Calculate the horizontal distance by using the following formula
Distance = Map distance in mm x map scale
1000 OR 1 000 000
Divide by a thousand if you want the distance in meters OR a 1 000 000 if you need the answer in kilometres
In this instance we will need the distance in meters!
E.g. the map distance between Point A and Point B is 23mm
Distance = 23mm x 50 000
1000
= 1150000
1000
= 1150m
Step 3: Gradient calculation
Gradient can be expressed in a fraction (e.g. 1:25) format or as a percentage (%)
Gradient = Vertical difference
Horizontal distance
= 260m
1150m
= 260m ÷ 260
1150m ÷ 260
= 1 .
4,42
1:4.42
Therefore, for every 4.42 meters you are moving horizontally the height will change by 1 meter. This is quite steep!!
How to calculate Time:
Step 1: Calculate the distance between point A and point B in kilometers, because the speed is in kilometers per hour.
You will notice that every decimal has been converted into a smaller unit. E.g. 3,58 hours, is 3hours (,58 x 60 = 34,8 minutes and .8 minutes x 60 = 48 seconds)
